การวิเคราะห์และการตีความหมายข้อมูล (Analysis and Interpretation of Data)

          ข้อมูลที่ทำการเก็บรวบรวม โดยทั่วไปจะมีจำนวนมาก เมื่อได้ข้อมูลมาแล้ว ก็จะมีการดำเนินกับข้อมูลด้วยวิธีการต่างๆ เช่น การแยกประเภท การจัดชั้น การสังเขป การหาข้อสรุปเกี่ยวกับลักษณะต่างๆ ของข้อมูล การพิจารณาหาว่าข้อมูลที่เก็บรวบรวมมาได้มีความสัมพันธ์กับข้อมูลอื่นหรือไม่อย่างไร ตลอดจนอาจทำการพยากรณ์เหตุการณ์ในอนาคตจากข้อมูลที่เก็บรวบรวมได้ กระบวนการต่างๆ เหล่านี้เรียกว่า การวิเคราะห์ข้อมูล  ซึ่งจะดำเนินการในรายละเอียดอย่างไรและเพียงไรนั้นขึ้นอยู่กับลักษณะของข้อมูล และเรื่องที่ต้องการศึกษา ในบางกรณี การวิเคราะห์ข้อมูลก็ทำโดยใช้กราฟ ดังนั้นเมื่อพิจารณาให้ดีจะเห็นว่าบางขั้นตอนของการวิเคราะห์ข้อมูล เช่นการจัดชั้นหรือแยกประเภทของข้อมูล จะต้องเตรียมวางแผนพร้อมกันไปกับการเก็บรวบรวมและการนำเสนอข้อมูล
          เมื่อข้อมูลได้รับการวิเคราะห์แล้ว ขั้นสุดท้ายของการดำเนินการทางสถิติก็คือ การตีความหมายข้อมูลเหล่านั้น การตีความหมายก็คือ การพิจารณาหาว่าอะไรคือข้อสรุปที่ได้จากการวิเคราะห์ ตัวเลขที่ได้จากการวิเคราะห์ช่วยสนับสนุนหรือปฏิเสธสมมุติฐานที่ตั้งไว้เกี่ยวกับเรื่องนั้นๆ และตัวเลขที่ได้จากการวิเคราะห์บอกอะไรบางอย่างใหม่ๆ แก่เราบ้าง
          การตีความหมายข้อมูลเป็นเรื่องที่ทำได้ไม่ง่ายนัก เนื่องด้วยความรู้และเอกสารเกี่ยวกับเรื่องที่เกี่ยวข้องมักมีจำกัด ดังนั้นการตีความหมายข้อมูล จึงไม่ควรสรุปลงไปอย่างแน่นอนตายตัวว่าต้องเป็นอย่างนั้นอย่างนี้ นอกจากนั้นเหตุผลอีกประการหนึ่งที่สนับสนุนการกระทำดังกล่าวนี้ ก็คือตัวข้อมูลเอง ได้เคยกล่าวไว้แล้วว่า ข้อมูลประกอบด้วยข้อเท็จและข้อจริง มิใช่ข้อจริงล้วนๆ และตัวเลขที่ได้จากการวิเคราะห์ก็เป็นเพียงค่าประมาณ ดังนั้นการตีความหมายข้อมูลโดยการสรุปอย่างแน่นอนตายตัว จึงมีโอกาสผิดพลาดได้ง่ายมาก
          อย่างไรก็ตาม การตีความหมายที่ดี ขึ้นอยู่กับหลักเกณฑ์ 4 ประการ ดังต่อไปนี้
          1.  มีความตั้งใจแน่วแน่ที่จะค้นหาความจริงทุกอย่างที่ซ่อนเร้นอยู่ในข้อมูล
          2.  มีความรู้ความเข้าใจอย่างกว้างขวางในเหตุการณ์หรือเรื่องที่กำลังศึกษา
          3.  มีความคิดที่เป็นระเบียบและมีเหตุผลในการทำงาน
          4.  มีความสามารถในการใช้ถ้อยคำที่ชัดเจน ทำให้อ่านเข้าใจได้ง่าย

         กระบวนการต่างๆ  ของการวิเคราะห์ข้อมูล แยกกล่าวเป็นข้อๆ ได้ดังต่อไปนี้

          ข้อมูลที่เก็บรวบรวมมาได้ อาจมีมากประเภทหรือน้อยประเภท แล้วแต่เรื่องที่ต้องการศึกษา ตัวอย่างข้อมูลเกี่ยวกับชาวนา เช่น จำนวนชาวนา เนื้อที่เพาะปลูกและผลิตผลของข้าว รายได้ เป็นต้น ข้อมูลแต่ละประเภทเหล่านี้อาจจำแนกเป็นชนิดย่อยออกไปอีก ทั้งนี้เพื่อจะได้ศึกษาในรายละเอียดปลีกย่อยต่างๆ ให้มากขึ้นตามความต้องการ เช่น จำนวนชาวนา อาจจำแนกตามเพศ อายุ และชั้นการศึกษา เนื้อที่เพาะปลูกและผลิตผลข้าวอาจจำแนกออกเป็นข้าวเจ้า และข้าวเหนียว รายได้อาจจำแนกตามแหล่งที่มา เช่น เงินที่ได้จากการขายข้าว ค่าเช่าที่นา ค่าแรงงานรับจ้าง เป็นต้น
          การแยกประเภทข้อมูล อาจเป็นขั้นตอนที่พอเพียงสำหรับการวิเคราะห์ข้อมูลบางอย่างซึ่งไม่ต้องการศึกษาข้อมูลในขั้นลึกซึ้งนัก แต่สำหรับการศึกษาบางอย่าง การแยกประเภทข้อมูลเป็นเพียงขั้นเตรียมงานเท่านั้น ซึ่งในประการหลังนี้ลักษณะต่างๆ ของข้อมูลทั้งที่เป็นรายข้อมูล และในส่วนรวมจะต้องได้รับการพิจารณาและศึกษาอย่างละเอียดละออ
[กลับหัวข้อหลัก]

          ข้อมูลที่เก็บรวบรวมมาได้ในขั้นแรกจะอยู่ในสภาพที่ไม่เป็นระเบียบเรียบร้อย ยังไม่สามารถทำการหาข้อสรุปของลักษณะต่างๆ ของข้อมูลได้ ข้อมูลที่อยู่ในรูปเช่นนี้มีชื่อเรียกว่า "ข้อมูลดิบ" (Raw data) ดังนั้นเพื่อให้ข้อมูลอยู่ในสภาพพร้อมที่จะสามารถหาข้อสรุปหรือทำการวิเคราะห์โดยวิธีอื่นๆ ได้ จึงอาจดำเนินการสังเขปข้อมูลดิบ หรือจัดข้อมูลดิบทั้งสิ้นให้อยู่ในรูปแบบใหม่ซึ่งเป็นระเบียบเรียบร้อย และมีขนาดกะทัดรัดสะดวกต่อการดำเนินการวิเคราะห์ในขั้นต่อไป การสังเขปข้อมูลตามที่กล่าวมานี้เรียกว่า "การแจกแจงความถี่" (Frequency distribution)
          ในกรณีที่ข้อมูลมีจำนวนไม่มากนัก การแจกแจงความถี่อาจแสดงเป็นรายข้อมูลที่เก็บรวบรวมมาได้ พร้อมทั้งความถี่หรือจำนวนที่ซ้ำๆ กันของข้อมูลตัวนั้นๆ
          ตัวอย่าง  นักเรียน  40  คน  สอบไล่วิชาเลขคณิตได้คะแนน  ดังต่อไปนี้
          15   23   25   27   19   20   19   17
          18   24   23   26   29   25   21   23
          25   25   25   25   24   17   20   25
          28   26   25   20   22   22   26   26
          20   22   22   21   19   27   24   24

          ข้อมูลข้างต้นนี้ เรียกว่า ข้อมูลดิบ เมื่อแจกแจงความถี่เป็นรายข้อมูลจะได้ดังนี้

คะแนน	ความถี่
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29	1 – 2 1 3 4 2 4 3 5 7 4 2 1 1
รวม	40

          การแจกแจงความถี่ที่ได้แสดงไว้ข้างบนนี้ ถ้าข้อมูลมีจำนวนมาก ตารางดังกล่าวจะยากมาก ทำให้ต้องเสียเนื้อที่กระดาษ และไม่สะดวกที่จะทำการวิเคราะห์ในขั้นต่อไป นอกจากนี้ถ้าจะพิจารณาในด้านการกระจายของข้อมูลว่า ข้อมูลส่วนใหญ่มีค่าระหว่างเท่าไรถึงเท่าไร หรือรูปลักษณะการกระจายข้อมูลเป็นอย่างไร ก็จะไม่สามารถแลเห็นรูปลักษณะของการกระจายได้ชัดเจน ดังนั้น จึงอาจจะจัดทำการแจกแจงความถี่ของข้อมูลให้อยู่ในรูปใหม่ ซึ่งมีลักษณะอัดแน่นกว่าตารางข้างต้น กล่าวคือ จัดข้อมูลให้รวมอยู่เป็นกลุ่มๆ แล้วดูว่าข้อมูลค่าต่างๆ อยู่ในกลุ่มหรือชั้นใดบ้าง ให้นับจำนวนข้อมูลเหล่านั้นว่าอยู่ในชั้นใด เป็นจำนวนเทาใด จำนวนข้อมูลในแต่ละชั้นเรียกว่า ความถี่
          อย่างไรก็ตาม ถ้าจัดกลุ่มข้อมูลแต่ละกลุ่มให้มีขนาดใหญ่มาก จำนวนกลุ่มหรือจำนวนชั้นก็จะมีน้อย และจำนวนข้อมูลในแต่ละกลุ่มก็จะอัดกันแน่นมากเกินไป ทำให้ไม่สามารถแลเห็นลักษณะการกระจายของข้อมูลได้ดี แต่ถ้าหากจัดแต่ละกลุ่มให้มีขนาดเล็กมาก จำนวนกลุ่มหรือจำนวนชั้นก็จะมีมาก ซึ่งจะทำให้การกระจายของข้อมูลมีลักษณะแผ่กว้างมากเกินไป  ไม่ช่วยให้แลเห็นลักษณะการกระจายที่ดี  ดังนั้นการแจกแจงความถี่แบบจัดข้อมูลให้เป็นกลุ่มๆ นี้ จึงต้องให้แต่ละกลุ่มมีขนาดโตพอดี ที่จะทำให้แลเห็นลักษณะการกระจายของข้อมูลได้อย่างเด่นชัด กล่าวคือข้อมูลในกลุ่มจะต้องไม่อัดแน่นมากเกินไป และก็ต้องไม่แผ่กระจายมากจนเกินไปด้วย
          ตารางข้างล่างนี้ เป็นตารางการแจกแจงความถี่ที่ได้จัดข้อมูลเป็นกลุ่มๆโดยได้ใช้ข้อมูลที่ให้ไว้ข้างต้น ตารางดังกล่าวนี้เป็นแบบอย่างของตารางทั่วไป ที่ใช้ในการวิเคราะห์ข้อมูล

คะแนน	ความถี่
15-17 18-20 21-23 24-26 27-29	3 8 9 16 4
รวม	40

          ข้อมูลแต่ละชุดที่เก็บรวบรวมมาได้ อาจมีรูปลักษณะของการแจกแจงความถี่ไม่เหมือนกัน ลักษณะการแจกแจงความถี่ที่พบมากที่สุด ได้แก่ข้อมูลที่มีค่ากลางๆ มีจำนวนมาก ส่วนข้อมูลที่มีค่าสูง และที่มีค่าต่ำมีจำนวนน้อย ถ้านำข้อมูลประเภทนี้มาเขียนกราฟจะได้รูปโค้ง ดังแสดงไว้ในรูปที่ 1 รูปที่  2 และรูปที่ 3 
          รูปที่ 1แสดงให้เห็นว่าข้อมูลที่มีค่ามาก และข้อมูลที่มีค่าน้อย เมื่อนับจากข้อมูลที่มีค่ากลางจะมีจำนวนเท่าๆ กัน ดูจากรูปจะเห็นว่าปลายทั้งสองข้างของโค้งมีลักษณะสมมาตร (Symmetrical) รูปการแจกแจงความถี่ของข้อมูลที่มีลักษณะเช่นนี้ เรียกว่า โค้งปกติ (Normal curve) หรือโค้งรูประฆังคว่ำ
          สำหรับรูปที่ 2 และรูปที่ 3 นั้น เป็นการแจกแจงความถี่ของข้อมูลที่มีลักษณะที่เรียกว่ามีความเบ้ (Skewness) นั่นคือข้อมูลค่าน้อยมีจำนวนมากกว่าข้อมูลที่มีค่ามาก หรือที่เรียกว่าเบ้ไปทางบวก (Positively skewed) ซึ่งได้แก่รูปที่  2และข้อมูลค่ามาก มีจำนวนมากกว่าข้อมูลที่มีค่าน้อย หรือที่เรียกว่าเบ้ไปทางลบ (Negatively skewed) ซึ่งได้แก่รูปที่  3 การแจกแจงความถี่ของข้อมูลลักษณะอื่นที่จะยกมาให้ดู นอกจากนี้ก็มีรูปสี่เหลี่ยมผืนผ้า(รูปที่ 4) รูปตัว U (รูปที่ 5) รูปตัว J (รูปที่ 6) และรูปตัว J กลับ (รูปที่ 7)
[กลับหัวข้อหลัก]

          ข้อมูลแต่ละชุดที่เก็บรวบรวมมาได้ อาจมีลักษณะการแจกแจงความถี่แตกต่างกันไปดังได้กล่าวแล้วในข้อ 2 ในการวิเคราะห์ข้อมูล เราจำเป็นต้องศึกษาอย่างละเอียดละออว่าข้อมูลชุดนั้นๆ บอกอะไรแก่เราบ้าง เช่น สมมุติว่ามีข้อมูลเกี่ยวกับรายได้ต่อปีของคนจำนวนหนึ่งซึ่งเป็นตัวอย่างของประชากรทั้งประเทศ สิ่งต่างๆ ที่อาจต้องการทราบก็คือ ประชากรมีรายได้ต่อปีเฉลี่ยคนละเท่าไร รายได้ของคนมั่งมีและคนยากจนแตกต่างกันมากหรือไม่ และถ้าคนส่วนใหญ่ค่อนข้างยากจน คนเหล่านี้มีมากเพียงไร ค่าเหล่านี้คือค่าซึ่งบอกลักษณะต่างๆ ของข้อมูลซึ่งเป็นค่าสถิติอย่างหนึ่ง และสามารถคำนวณหาได้
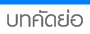
          อันที่จริงค่าต่างๆ เหล่านี้ พอจะทราบได้อย่างคร่าวๆ จากลักษณะการแจกแจงความถี่ของข้อมูล สมมุติว่ารูปที่ 8 ได้จากการแจกแจงความถี่ของรายได้ต่อปีของประชากรตามที่กล่าวข้างต้น สิ่งที่ทราบได้อย่างคร่าวๆ จากรูปดังกล่าวก็คือ  ประชากรที่มีรายได้ปานกลางค่อนไปทางข้างต่ำมีจำนวนมาก ส่วนประชากรที่มีรายได้ต่ำมากหรือสูงมากมีจำนวนน้อย  นอกจากนั้นช่องว่างระหว่างคนร่ำรวยและคนยากจนกว้างมาก ทั้งนี้เพราะปลายทั้งสองข้างของรูปโค้งห่างกันมาก อย่างไรก็ตามในทางสถิติ ข้อสรุปที่มิใช่ตัวเลขมีความหมายน้อยและไม่สามารถจะนำไปใช้ประโยชน์ในขั้นต่อไปได้ ดังนั้น ข้อสรุปทั้งหลายของข้อมูลจึงต้องแสดงออกเป็นตัวเลข
          เนื่องจากการแจกแจงความถี่ของข้อมูลที่พบส่วนมาก มีลักษณะเป็นโค้งรูประฆัง กล่าวคือตรงกลางป่อง และโค้งจะลาดลงทั้งสองข้าง ดังนั้นการหาค่าที่บอกลักษณะสำคัญของข้อมูลที่มีการกระจายลักษณะนี้ ได้แก่การหาค่ากลางและการหาค่าการกระจายของข้อมูล ซึ่งจะได้กล่าวเป็นเรื่องๆ ต่อไป
          1.  การหาค่ากลางของข้อมูล
          ค่ากลางของข้อมูลซึ่งมีที่ใช้มากได้แก่ มัชฌิมเลขคณิต (Arithmetic Mean) มัธยฐาน (Median) และฐานนิยม(Mode)
          ก)  มัชฌิมเลขคณิตของข้อมูลชุดใดๆ คือค่าเฉลี่ยของข้อมูลชุดนั้น ซึ่งอาจเขียนให้อยู่ในรูปสูตรได้ดังนี้
          มัชฌิมเลขคณิต  =   ผลบวกของทุกค่าของข้อมูล
                                                           จำนวนข้อมูล
          ข)  มัธยฐานของข้อมูลชุดใดๆ คือ คะแนนหรือค่า ณ ตำแหน่งกึ่งกลางของข้อมูลชุดนั้น ซึ่งข้อมูลทั้งชุดได้รับการเรียงลำดับแล้ว
          ค)  ฐานนิยมของข้อมูลชุดใดๆ คือ คะแนนหรือค่าที่มีความถี่สูงสุด หรือซ้ำกันมากที่สุดของข้อมูลชุดนั้น

         ตัวอย่าง จงหามัชฌิมเลขคณิต  มัธยฐาน และฐานนิยมของข้อมูลต่อไปนี้ 7   7   8   9   13   13   13
         มัชฌิมเลขคณิต  =  ผลบวกของทุกค่าของข้อมูล
                                                         จำนวนข้อมูล
                                   =  (7  +  7  +  8  +  9  +  13  +  13  +  13)
                                                                               7
                                   =  10
           มัธยฐาน             =   9
          ฐานนิยม              =  13

          2. การหาค่าการกระจายข้อมูล
          การกระจายของข้อมูล หมายถึงการที่ข้อมูลชุดหนึ่งชุดใดมีลักษณะแผ่กว้างออกไปตามแนวนอนของแกนพิกัดฉากของกราฟ
          สมมุติว่ามีคะแนนซึ่งได้จากการสอบคิดเลขในใจของเด็ก 20  คน ซึ่งแบ่งเป็น 2 กลุ่ม กลุ่มละ 10  คน  ดังนี้
          กลุ่มที่ 1 ได้คะแนน  4  8  5  6  7  10  2  7  6  8
          กลุ่มที่ 2 ได้คะแนน  6  7  6  5  4   6  7  6  8  5
          ถ้านำข้อมูลทั้งสองชุดนี้มาลงจุด จะเห็นว่าคะแนนของนักเรียนกลุ่มที่ 1 มีลักษณะแผ่กว้างออกไปหรือมีการกระจายมากกว่าคะแนนของนักเรียนกลุ่มที่ 2 ดังแสดงด้วยรูปที่ 9  และรูปที่ 10
          วิธีที่ง่ายที่สุดที่จะเปรียบเทียบระหว่างข้อมูล 2  ชุดว่าข้อมูลชุดใดมีการกระจายมากกว่ากัน ได้แก่การตรวจดูค่าแตกต่างระหว่างคะแนนค่าสูงสุด และคะแนนค่าต่ำสุดของข้อมูลแต่ละชุด ค่าแตกต่างดังกล่าวนี้มีชื่อเรียกว่า "พิสัย" (Range) ข้อมูลชุดใดมีค่าพิสัยสูงกว่า แสดงว่าข้อมูลนั้นน่าจะมีการกระจายมากกว่า
          จากตัวอย่างข้อมูลที่ยกมาข้างต้นนี้จะเห็นว่า
           ข้อมูลกลุ่มที่  1 พิสัย  =  10 - 2 = 8
           ข้อมูลกลุ่มที่  2 พิสัย  =   8 - 4 = 4
           เนื่องจากพิสัยเป็นสถิติที่ใช้วัดการกระจายได้อย่างคร่าวๆ เท่านั้น ดังนั้นจึงมักไม่เป็นที่นิยมใช้กัน
           สถิติวัดการกระจายที่สำคัญ และใช้กันทั่วไป คือ ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) ซึ่งหาได้จากการเอาผลต่างระหว่างข้อมูลแต่ละค่า และมัชฌิมเลขคณิตของข้อมูลนั้นมายกกำลังสอง แล้วทำการถัวเฉลี่ยค่ากำลังสองเหล่านั้น จากนั้นจึงถอดกรณฑ์ที่สองของค่าเฉลี่ยที่ได้
           จากข้อมูลกลุ่มที่  2  หาค่าส่วนเบี่ยงเบนมาตรฐานได้ดังนี้
            มัชฌิมเลขคณิต      =  6  +  7  +  6  +  5  +  4  +  6  +  7  +  6  +  8  +  5
                                                                                          10
                                    =  60
                                                      10
                                    =   6
           ส่วนเบี่ยงเบนมาตรฐาน  =  6-6)²+(7-6)²+(6-6)²+(5-6)²+...+(5-6)²))/10
                                         = (0+1+0+1+4+0+1+0+4+1)/10
                                         = 12/10
                                         =  1.2
                                         =    1.1

          ค่าที่ได้จากการวัดการกระจายของข้อมูล เป็นสถิติสำคัญที่นำไปใช้ประโยชน์อย่างกว้างขวาง  ค่าปานกลางเพียงอย่างเดียวไม่สามารถใช้บรรยายลักษณะสำคัญของข้อมูลทั้งกลุ่มได้เพียงพอ เช่นคนกลุ่มหนึ่งมีรายได้เฉลี่ยค่อนข้างสูง แต่มิได้หมายความว่าทุกคนในกลุ่มนั้นจะต้องมีรายได้สูงไปด้วย อาจจะมีบางคนซึ่งมีรายได้สูงมากและต่ำมากรวมอยู่ด้วย หรือทั้งกลุ่มอาจจะมีรายได้ไล่เลี่ยกันไม่แตกต่างกันมากนักก็เป็นได้ ลักษณะเช่นที่ว่านี้จะต้องดูจากการกระจายของข้อมูลซึ่งบางกลุ่มก็มีการกระจายมาก บางกลุ่มก็มีน้อย
          นอกจากนี้ประโยชน์ที่ได้จากการกระจายของข้อมูล ก็คือการนำไปใช้ในการควบคุมคุณภาพของผลิตภัณฑ์บางอย่าง   โดยพิจารณากำหนดว่า สิ่งของที่ผลิตได้ อาจจะเบี่ยงเบนไปจากคุณภาพมาตรฐานได้บ้าง แต่ต้องไม่เกินเท่าไร และทำนองเดียวกัน ในด้านของการพยากรณ์ก็จะสามารถใช้ค่าการกระจายเป็นตัวกำหนดได้ว่า การพยากรณ์นั้นๆ จะเชื่อถือได้มากน้อยเพียงไร และถ้าจะพยากรณ์คลาดเคลื่อนจากความจริงไปบ้างจะไม่มากหรือน้อยกว่าเท่าไร เป็นต้น
[กลับหัวข้อหลัก]

          ข้อมูลบางชนิดแสดงถึงเหตุการณ์ที่เกิดขึ้นเป็นรายคาบเวลา เช่น ปริมาณสินค้าส่งออกเป็นรายปี จำนวนอุบัติเหตุรถยนต์บนท้องถนนเป็นรายสัปดาห์ ปริมาณน้ำฝนที่ตกเป็นรายเดือน เป็นต้น ข้อมูลประเภทนี้เรียกว่าข้อมูลอนุกรมเวลา(Time-series data)
          ถ้านำข้อมูลประเภทนี้ที่เกิดขึ้นในช่วงเวลาหนึ่งซึ่งยาวนานพอสมควรมาลงจุดจะได้เส้นกราฟ ซึ่งมีลักษณะโดยส่วนรวมอาจชันขึ้นหรือลาดลง หรือมีทั้งชันขึ้นหรือลาดลงในช่วงเวลาหนึ่งเช่นในรอบ 1 ปี เป็นต้น ลักษณะโดยส่วนรวมที่ชันขึ้นหรือลาดลงของเส้นกราฟในช่วงเวลายาวนานนี้ เรียกว่า แนวโน้มของข้อมูล
          วิธีการหาแนวโน้มของข้อมูลอาจแบ่งได้เป็น 2 วิธีใหญ่ๆ คือ
          1)  วิธีการกะประมาณ  ซึ่งโดยมากใช้การลากเส้นอย่างอิสระ (Freehand method)
          2)  วิธีการคำนวณ ที่นิยมใช้ก็มีการถัวเฉลี่ยเคลื่อนที่ (Moving average method) และวิธีกำลังสองน้อยทีสุด (Least squares method) ซึ่งวิธีหลังนี้จะได้แนวโน้มอยู่ในรูปของสมการ

          1. การลากเส้นอย่างอิสระ
            การสร้างแนวโน้มด้วยวิธีนี้ คือ การลากเส้น ซึ่งเป็นแนวเรียบผ่านไปในระหว่างเส้นกราฟของข้อมูล ซึ่งปกติจะมีบางตอนหักเหขึ้น และบางตอนหักเหลง เส้นซึ่งเป็นแนวเรียบนี้แสดงถึงความเป็นไปโดยส่วนรวมในระยะยาวของเหตุการณ์ทั้งหมดที่เกิดขึ้นซึ่งเราเรียกว่า แนวโน้มของข้อมูล การลากเส้นอย่างอิสระนี้ไม่มีกฎเกณฑ์ใดๆ ทั้งสิ้น นอกจากคอยระมัดระวังให้แนวโน้มแสดงถึงเหตุการณ์ที่เกิดขึ้นในระยะยาวได้ถูกต้องเท่านั้น ดังแสดงด้วยรูป
         2. การถัวเฉลี่ยเคลื่อนที่
            สมมุติว่ามีข้อมูลจำนวนหนึ่งซึ่งเก็บรวบรวมไว้เป็นรายเดือน ถ้าเราหาค่ามัชฌิมเลขคณิตของข้อมูลในช่วงเวลาหนึ่งเช่น ในรอบ 3 เดือน เป็นต้น แล้วจดค่านี้ไว้ จากนั้นก็เลื่อนช่วงเวลา 3 เดือนนี้ต่อไปโดยตัดข้อมูลตัวแรกออกและเพิ่มข้อมูลตัวที่ 4 เข้ามา แล้วก็หามัชฌิมเลขคณิตของช่วงเวลาดังกล่าวนี้อีกและจดค่าที่คำนวณได้ไว้ ทำเช่นนี้เรื่อยๆ ไปก็จะได้ข้อมูลชุดใหม่  ซึ่งเป็นค่ามัชฌิมเลขคณิตของข้อมูลทุกๆ 3 เดือนต่อเนื่องกัน  วิธีการเช่นนี้เรียกว่าการถัวเฉลี่ยเคลื่อนที่ 3 เดือน ในข้อมูลบางชุดอาจทำการถัวเฉลี่ยเคลื่อนที่ทุก 5 เดือน หรือทุก 3 ปี หรือทุก 5 ปีก็ได้ ทั้งนี้ขึ้นอยู่กับชนิดและลักษณะของข้อมูล
          เมื่อนำค่ามัชฌิมเลขคณิตเคลื่อนที่ที่ได้นี้มาลงจุด แล้วโยงจุดต่างๆ เหล่านี้ ก็จะได้เส้นซึ่งแสดงแนวโน้มของข้อมูลเป็นรายเดือน ตารางข้างล่างนี้เป็นการคำนวณหาแนวโน้มของราคาเฉลี่ยต่อเกวียนของข้าวเปลือกเจ้าชั้นพิเศษ 100% ที่ซื้อขายกันในตลาดกรุงเทพมหานครระหว่างเดือนมกราคมถึงธันวาคม 2522 โดยวิธีการถัวเฉลี่ยเคลื่อนที่ 3 เดือน

(ตัวเลขมีหน่วยเป็นบาท)

เดือน	ราคาเฉลี่ยต่อเกวียน ของข้าวเปลือกเจ้า ชั้นพิเศษ 100%	ผลรวมเคลื่อนที่ 3 เดือน	มัชฌิมเลขคณิต เคลื่อนที่ 3 เดือน
มกราคม     กุมภาพันธ์     มีนาคม     เมษายน     พฤษภาคม     มิถุนายน     กรกฎาคม     สิงหาคม     กันยายน     ตุลาคม     พฤศจิกายน     ธันวาคม	2,520 2,581 2,660 2,736 2,757 2,831 2,774 2,916 3,171 3,252 3,184 3,237	- 7,761 7,977 8,153 8,324 8,362 8,521 8,861 9,339 9,607 9,673 -	- 2,587.0 2,659.0 2,717.7 2,774.7 2,787.3 2,840.3 2,953.7 3,113.0 3,202.3 3,224.3 -

ที่มา :รายงานเศรษฐกิจ ธนาคารกรุงไทยจำกัด มิถุนายน 2522

          เมื่อนำเอาค่ามัชฌิมเลขคณิตเคลื่อนที่ 3 เดือนมาลงจุดจะได้แนวโน้มของราคาเฉลี่ยต่อเกวียนของข้าวเปลือกเจ้าชั้นพิเศษ 100% ในรอบปี
พ.ศ. 2522 ดังแสดงในรูป
          อันที่จริงเส้นที่ได้นี้ จะไม่ถือว่าเป็นแนวโน้มก็ได้เพราะมิได้แสดงถึงแนวโน้มของเหตุการณ์ที่เกิดขึ้นในระยะยาวอย่างแท้จริง หากแต่เป็นเส้นซึ่งช่วยลดการกระเพื่อมขึ้นลงของเส้นกราฟอันเกิดจากข้อมูลเดิมให้เรียบขึ้นเท่านั้น แนวโน้มของข้อมูลเป็นเครื่องมืออย่างหนึ่งที่ใช้ในการพยากรณ์ ส่วนที่ต่อจากปลายแนวโน้มออกไปคือ คำพยากรณ์ ดังนั้นถ้าทำการวิเคราะห์ข้อมูลด้วยการศึกษาแนวโน้มอย่างละเอียดลออทุกแง่ทุกมุมแล้วจะช่วยเพิ่มความแม่นยำให้แก่การพยากรณ์ยิ่งขึ้น

[กลับหัวข้อหลัก]

          เมื่อเอ่ยคำว่า พยากรณ์ บางคนอาจนึกถึงโหร หรือหมอดู เพราะการพยากรณ์ก็คือการทำนายล่วงหน้า ซึ่งมักเป็นงานของโหร  แต่การพยากรณ์มิใช่งานผูกขาดของโหร ใครๆ ก็พยากรณ์ได้ ต่างกันก็แต่ว่าหลักเกณฑ์และวิธีการที่ใช้ในการพยากรณ์แตกต่างกันอย่างไรเท่านั้น การพยากรณ์ที่ทำกันโดยทั่วไปมีอยู่ 3 วิธี  คือ
          1.  พยากรณ์โดยอาศัยประสบการณ์และความชำนาญ วิธีนี้นิยมใช้กันมาก เนื่องจากไม่ต้องมีหลักเกณฑ์ที่แน่นอนอะไร เพียงแต่อาศัยประสบการณ์และความรู้ความชำนาญทางด้านนี้ ตลอดจนเข้าใจแจ่มแจ้งในปัญหาของเรื่องที่จะพยากรณ์ เช่นสมาคมผู้ค้าข้าวโพด ทำการประเมินผลผลิตข้าวโพดประจำปี โดยการส่งคณะเจ้าหน้าที่ออกไปตระเวนดูสภาพของต้นข้าวโพดในท้องที่ที่มีการปลูกข้าวโพดมากทั่วประเทศ แล้วเปรียบเทียบว่าสภาพต้นข้าวโพดในปีนี้ดีหรือเลวกว่าปีที่แล้วเพียงไร ปลูกในเนื้อที่มากขึ้นหรือลดลง จากนั้นก็พยากรณ์ผลผลิตข้าวโพด โดยใช้ผลผลิตของปีที่แล้วเป็นหลักว่าควรเพิ่มหรือลดลงเท่าไร
          อย่างไรก็ตาม การพยากรณ์ด้วยวิธีนี้ สามารถนำไปใช้ได้ในกรณีที่มีการดำเนินงานในขอบเขตขนาดเล็กเท่านั้น อนึ่ง การพยากรณ์ด้วยวิธีนี้แม้จะเป็นวิธีที่ง่าย แต่ก็มีโอกาสผิดพลาดได้มาก โดยเฉพาะอย่างยิ่งถ้าผู้พยากรณ์ไม่มีประสบการณ์ หรือขาดความรู้ความชำนาญเกี่ยวกับเรื่องที่จะทำการพยากรณ์
          2. พยากรณ์โดยอาศัยเหตุการณ์และหลักฐานบางอย่าง การพยากรณ์ด้วยวิธีนี้ มักมีการอภิปรายประกอบหลักฐานกันอย่างกว้างขวาง แล้วสรุปหาข้อยุติ หลักฐานเหล่านี้อาจเป็นหลักฐานทางนิติศาสตร์ ทางการเมือง ทางเศรษฐกิจและสังคม  ตัวอย่างเช่น เมื่อสงครามโลกครั้งที่สองได้สิ้นสุดลงก็มีผู้พยากรณ์ว่าจะเกิดภาวะข้าวยากหมากแพง โจรผู้ร้ายชุกชุม เช่นเดียวกับที่เคยเกิดมาแล้ว ภายหลังสงครามโลกครั้งที่หนึ่ง  เป็นต้น การพยากรณ์แบบนี้อาจกล่าวในเชิงคณิตศาสตร์ได้ว่า ตั้งอยู่บนรากฐานของ  "ตัวแปรที่วัดค่าไม่ได้"
          3. การพยากรณ์ทางสถิติ เป็นการพยากรณ์โดยใช้ข้อมูลสถิติประเภทที่เรียกว่า ข้อมูลอนุกรมเวลาเป็นเครื่องมือ  การพยากรณ์โดยวิธีนี้จะต้องศึกษาถึงพฤติการณ์ของเรื่องนั้นๆ ที่เกิดขึ้นในอดีตว่ามีลักษณะอย่างไรเสียก่อน แล้วจึงทำการพยากรณ์ ข้อมูลอนุกรมเวลาจะบอกให้ทราบถึงพฤติการณ์นั้นๆ ตัวอย่างของการพยากรณ์ทางสถิติในเรื่องที่เกี่ยวกับเศรษฐกิจ  และธุรกิจ ได้แก่ การพยากรณ์จำนวนประชากรของประเทศ การพยากรณ์ผลผลิตทางการเกษตร ปริมาณการขาย ระดับราคาสินค้า ฯลฯ เป็นต้น
          การพยากรณ์ทางสถิติจะทำได้ต่อเมื่อพฤติการณ์ที่เกิดขึ้นในอดีตมีความแปรผันตามปกติ เช่น แต่ละปีที่ผ่านไปจำนวนประชากรของโลกมีแนวโน้มเพิ่มขึ้นเรื่อยๆ หรืออัตราการตายของเด็กอายุต่ำกว่า 1 ปี มีแนวโน้มลดลงอย่างสม่ำเสมอ หรือสินค้าเครื่องกันหนาวจะขายได้มากในฤดูหนาว แต่จะขายได้น้อยในฤดูอื่นๆ เป็นต้น แต่ถ้าพฤติการณ์ที่เกิดขึ้นในอดีตมีความแปรผันผิดปกติ เช่น สินค้าเครื่องกันหนาว แทนที่จะขายได้น้อยในฤดูอื่นนอกจากฤดูหนาวเป็นประจำทุกปี กลับกลายเป็นว่าบางปีขายได้มาก บางปีก็ขายได้น้อย เอาแน่นอนอะไรไม่ได้ พฤติการณ์ทำนองนี้การพยากรณ์ทางสถิติไม่สามารถทำได้
          ตัวอย่างของการพยากรณ์จะดูได้จากรูปที่ 11 โดยต่อเส้นแนวโน้มออกไปค่าที่อ่านได้บนแกนตั้ง ณ ปีที่ต้องการ คือรายได้จากการขายผลิตภัณฑ์เคมีซึ่งคาดว่าบริษัท ดวงดี จำกัด จะได้รับโดยประมาณ ณ ปีนั้น
          การพยากรณ์ทางสถิติอาจทำได้โดยการคำนวณจากสมการของแนวโน้ม (หาได้โดยวิธีกำลังสองน้อยที่สุด) สมมุติว่าแนวโน้มที่แสดงในรูปที่ 11 มีสมการ เป็น
                    y   =   1.5 + 0.48 x
          เมื่อ     y   =   รายได้จากการขายผลิตภัณฑ์เคมีมีหน่วยเป็นแสนบาท
                    x   =   หน่วยแสดงเวลาเป็นปี  เริ่มจาก 0, 1, 2,3,...

          สมมุติว่าถ้าต้องการพยากรณ์รายได้จากการขายในปี พ.ศ.  2523 จะได้ค่า x  = 16 นำค่า x ไปแทนในสมการจะได้
                    y  =  1.5 + (0.48 x 16)
                        =  9.18
                       เนื่องจาก  y  มีหน่วยเป็นแสนบาท
                    y  =  9.18 x 100,000
                        =  918,000  บาท

          อย่างไรก็ตาม ค่าที่พยากรณ์ได้นี้เป็นเพียงค่าประมาณเท่านั้น ทั้งนี้เพราะการพยากรณ์ทางสถิติ ตั้งอยู่บนสมมุติฐานที่ว่า "สิ่งอื่นไม่เปลี่ยนแปลง" นั่นคือถือว่าเหตุการณ์อื่นๆ ที่จะเกิดขึ้นในช่วงเวลาของการพยากรณ์เหมือนกันกับที่เกิดขึ้นในช่วงเวลาที่แล้วๆ  มา แต่ความเป็นจริงมิได้เป็นเช่นนั้น เพราะเหตุการณ์ที่จะเกิดขึ้นในช่วงเวลาของการพยากรณ์น่าจะคล้ายคลึงกับเหตุการณ์ที่เพิ่มเกิดขึ้นเมื่อเร็วๆ นี้มากกว่าเหตุการณ์ที่เกิดขึ้นเมื่อนานมาแล้ว ยิ่งกว่านั้นในขณะที่จะทำการพยากรณ์หากบังเอิญไปอยู่ในวัฏจักร (Cycle) ที่เศรษฐกิจกำลังรุ่งเรืองถึงขีดสุด (Peak) ค่าที่พยากรณ์ได้จะสูงกว่าความเป็นจริง เพราะปกติวิสัยของเศรษฐกิจในช่วงเวลาถัดไปจะเริ่มตกต่ำ (Contraction) และในทางตรงข้าม ถ้าอยู่ในวัฏจักรที่เศรษฐกิจกำลังตกต่ำถึงที่สุด (Trough) ค่าที่พยากรณ์ได้ก็จะต่ำกว่าความเป็นจริง เพราะปกติวิสัยของเศรษฐกิจในช่วงเวลาถัดไปจะเริ่มฟื้นตัวดีขึ้น  (Expansion)
          นอกจากนี้เหตุการณ์ที่เกิดขึ้นโดยมิได้คาดหมายบางอย่าง เช่น การเกิดสงคราม การค้นพบสิ่งประดิษฐ์ใหม่ๆ รสนิยม  และทัศนคติของประชาชนที่เปลี่ยนแปลงไปก็มีส่วนกระทบกระเทือนต่อความถูกต้องของการพยากรณ์ด้วย เช่น ในการพยากรณ์ประชากรของโลกใน 10 ปีข้างหน้า หากเกิดสงครามขึ้นในระหว่างนี้ก็ดี หรือเกิดโรคระบาดอย่างใหม่ทำให้ผู้คนล้มตายเป็นจำนวนมากก็ดี กรณีเหล่านี้ก็ย่อมทำให้ค่าที่พยากรณ์ได้ต้องคลาดเคลื่อนจากความเป็นจริงไปได้
          อย่างไรก็ตาม แม้การพยากรณ์ทางสถิติจะมีข้อจำกัดในการใช้อยู่มากก็ตาม แต่เมื่อเปรียบเทียบกับวิธีการพยากรณ์ทั้งสองวิธีที่กล่าวมาแล้ว การพยากรณ์ทางสถิติก็จัดว่ามีหลักการและวิธีการที่ดีกว่า เพราะนอกจากจะต้องใช้ความรู้ความชำนาญและประสบการณ์เกี่ยวกับเรื่องที่จะพยากรณ์เหมือนสองวิธีที่กล่าวแล้ว การพยากรณ์ทางสถิติยังมีข้อมูลซึ่งแสดงถึงเหตุการณ์ต่างๆ ที่เกิดขึ้นในอดีต เป็นเครื่องชี้แนวทางพยากรณ์ นอกจากนั้นข้อมูลเหล่านี้ยังช่วยให้สามารถคำนวณได้ว่า ค่าที่พยากรณ์ได้อาจผิดพลาดจากความจริงได้ไม่เกินเท่าไร และสามารถเชื่อถือได้มากน้อยเพียงไรอีกด้วย ดังนั้นการพยากรณ์ทางสถิติ จึงนับว่าเป็นเครื่องมือที่สำคัญ และมีความจำเป็นต่อการกำหนดนโยบายและวางแผนงานบางอย่างทั้งของรัฐบาลและของเอกชนซึ่งจะขาดเสียมิได้

[กลับหัวข้อหลัก]