การพิจารณาค่าความจริง (Truth value)

          ประพจน์เดิมที่ถูกเปลี่ยนแปลงไปนั้น แยกพิจารณาความเป็นจริง หรือความเป็นเท็จได้ดังนี้

           ประพจน์ชนิดนี้เกิดขึ้นได้ด้วยการเติมคำ "ไม่" ซึ่งเขียนแทนด้วยสัญลักษณ์  "~"  ข้างหน้าประพจน์เดิม เช่น ก แทน มีทุเรียนอยู่ในกระจาด
         
          ~  ก  แทน  ไม่มีทุเรียนอยู่ในกระจาด ซึ่งจะมีกรณีที่เกิดขึ้นได้แตกต่างกัน 2 กรณี ดังนี้
          กรณีที่ 1  ก เป็นจริง เนื่องจากมีทุเรียนอยู่ในกระจาดจริงๆ ดังนั้น ~  ก เป็นเท็จ
          กรณีที่ 2  ก เป็นเท็จ (เนื่องจากไม่มีทุเรียนอยู่ในกระจาด) ดังนั้น  ~  ก เป็นจริง
          สรุปได้ว่า  กรณีที่ ก เป็นจริง  ~ ก จะเป็นเท็จ 
                       กรณีที่ ก เป็นเท็จ ~ ก  จะเป็นจริง

          เขียนแสดงด้วยตารางได้ดังนี้
   

	ก	~ ก
กรณีที่ 1	จริง	เท็จ
กรณีที่ 2	เท็จ	จริง

[กลับหัวข้อหลัก]

          ซึ่งเขียนแทนด้วยสัญลักษณ์ " ^ " ประพจน์ชนิดนี้เกิดขึ้นได้โดยการนำเอาประพจน์มาเชื่อมกันด้วย "และ" เช่น 
                 ก  แทน  "มีทุเรียนอยู่ในกระจาด"
                 ข  แทน  "มีมั่งคุดอยู่ในกระจาด"

         ประพจน์ที่เกิดขึ้นจากการเชื่อมประพจน์ ก ^ ข ด้วย "และ"  คือ "มีทุเรียนและมังคุดอยู่ในกระจาด" เขียนแทนด้วย "ก ^ ข"  จะมีกรณีที่เกิดขึ้นได้แตกต่างกัน 4 กรณีดังนี้

        กรณีที่ 1    ก  เป็นจริง
                         ข  เป็นจริง
                         ประพจน์ "มีทุเรียนและมังคุดอยู่ในกระจาด" เป็นจริง
        กรณีที่ 2     ก  เป็นจริง
                         ข  เป็นเท็จ
                         ประพจน์ "มีทุเรียนและมังคุดอยู่ในกระจาด" เป็นเท็จ
        กรณีที่ 3      ก  เป็นเท็จ
                         ข  เป็นจริง
                         ประพจน์  "มีทุเรียนและมังคุดอยู่ในกระจาด" เป็นเท็จ
        กรณีที่ 4     ก  เป็นเท็จ
                         ข  เป็นเท็จ
                         ประพจน์ "มีทุเรียนและมังคุดอยู่ในกระจาด" เป็นเท็จ

         สรุปได้ว่า กรณีที่ ก เป็นจริง ข เป็นจริง ประพจน์  ก ^ ข เป็นจริงกรณีอื่นๆ นอกจากนี้  ก ^ ข เป็นเท็จ

         เขียนแสดงด้วยตารางได้ดังนี้

	ก	ข	ก ^ ข
กรณีที่ 1	จริง	จริง	จริง
กรณีที่ 2	จริง	เท็จ	เท็จ
กรณีที่ 3	เท็จ	จริง	เท็จ
กรณีที่ 4	เท็จ	เท็จ	เท็จ

[กลับหัวข้อหลัก]

          ซึ่งเขียนแทนด้วยสัญลักษณ์ "v" ประพจน์ชนิดนี้เกิดขึ้นได้โดยการนำเอาประพจน์ทั้งสองมาเชื่อมกันด้วย "หรือ"
          สำหรับความหมายของคำ "หรือ" ในทางตรรกวิทยานั้น เมื่อเชื่อมประพจน์สองประพจน์ด้วย "หรือ" แล้ว จะมีความหมายถึงประพจน์ใดประพจน์หนึ่ง หรือทั้งสองประพจน์เลยก็ได้

          ดังนั้นประพจน์ "มีทุเรียนหรือมังคุดอยู่ในกระจาด" จึงมีความหมายเช่นเดียวกับ "มีทุเรียนหรือมังคุดอย่างน้อยหนึ่งอย่างอยู่ในกระจาด"
          ให้   ก  แทน  "มีทุเรียนอยู่ในกระจาด"
               ข  แทน  "มีมังคุดอยู่ในกระจาด"
               ประพจน์ที่เกิดขึ้นจากการเชื่อมประพจน์ ก,ข ด้วย "หรือ" คือ "มีทุเรียนหรือมังคุดอยู่ในกระจาด"  ซึ่งเขียนแทนด้วย "ก v ข"  ซึ่งจะมีกรณีที่เกิดขึ้นได้แตกต่างกัน 4 กรณี ดังนี้

          กรณีที่ 1    ก  เป็นจริง
                          ข  เป็นจริง
                          ประพจน์ "มีทุเรียนหรือมังคุดอยู่ในกระจาด" (อย่างน้อยหนึ่งอย่าง) เป็นจริง
          กรณีที่ 2    ก  เป็นจริง
                          ข  เป็นเท็จ
                          ประพจน์ "มีทุเรียนหรือมังคุดอยู่ในกระจาด" (อย่างน้อยหนึ่งอย่าง) เป็นจริง
          กรณีที่ 3    ก  เป็นเท็จ
                          ข  เป็นจริง
                          ประพจน์ "มีทุเรียนหรือมังคุดอยู่ในกระจาด" (อย่างน้อยหนึ่งอย่าง) เป็นจริง
          กรณีที่ 4    ก  เป็นเท็จ
                          ข  เป็นเท็จ
                          ประพจน์ "มีทุเรียนหรือมังคุดอยู่ในกระจาด" (อย่างน้อยหนึ่งอย่าง) เป็นเท็จ

          สรุปได้ว่ากรณีที่ ก เป็นเท็จ ข เป็นเท็จ ประพจน์  ก v ข จะเป็นเท็จ กรณีอื่นๆ นอกจากนี้  ก v ข เป็นจริง

          เขียนแสดงด้วยตารางได้ดังนี้

	ก	ข	ก v ข
กรณีที่ 1	จริง	จริง	จริง
กรณีที่ 2	จริง	เท็จ	จริง
กรณีที่ 3	เท็จ	จริง	จริง
กรณีที่ 4	เท็จ	เท็จ	เท็จ

[กลับหัวข้อหลัก]

          ซึ่งเขียนแทนด้วยสัญลักษณ์ "  → " ข้อความชนิดนี้เกิดขึ้นโดยการนำเอาประพจน์ทั้งสองมาเชื่อมกันด้วย "ถ้า...แล้วจะได้... " โดยมีประพจน์หนึ่งเป็นเหตุและอีกประพจน์หนึ่งเป็นผล  เช่น
          ก  แทน  "นายแดงซื้อทุเรียน"
          ข  แทน  "นายแดงได้รับทุเรียน"

          ประพจน์ที่เกิดขึ้นจากการเชื่อมประพจน์ ก,ข ด้วย "ถ้า...แล้วจะได้..." คือ "ถ้านายแดงซื้อทุเรียนแล้ว นายแดงจะได้รับทุเรียน" ซึ่งเขียนแทนด้วย "ก → ข" จะเห็นว่าประพจน์ ก เป็นเหตุ ประพจน์ ข  เป็นผล ซึ่งจะมีกรณีที่เกิดขึ้นได้แตกต่างกัน 4 กรณี ดังนี้

          กรณีที่ 1
          ก  เป็นจริง  (เพราะ ก  แทนนายแดงซื้อทุเรียน)
          ข  เป็นจริง  (เพราะ ข  แทนนายแดงได้รับทุเรียน)
          ประพจน์ "ถ้านายแดงซื้อทุเรียนแล้วนายแดงจะได้รับทุเรียน" เป็นจริง
          กรณีที่ 2
          ก  เป็นจริง  (เมื่อนายแดงซื้อทุเรียน)
          ข  เป็นเท็จ  (เมื่อนายแดงไม่ได้รับทุเรียน)
          ประพจน์ "ถ้านายแดงซื้อทุเรียนแล้วนายแดงจะได้รับทุเรียน" เป็นเท็จ
          กรณีที่ 3
          ก  เป็นเท็จ  (เมื่อนายแดงไม่ซื้อทุเรียน)
          ข  เป็นเท็จ  (เมื่อนายแดงได้รับทุเรียน)
          ประพจน์ "ถ้านายแดงซื้อทุเรียนแล้วนายแดงจะได้รับทุเรียน" ยังเป็นจริงอยู่
          กรณีที่ 4
          ก  เป็นเท็จ  (เมื่อนายแดงไม่ซื้อทุเรียน)
          ข  เป็นเท็จ  (เมื่อนายแดงไม่ได้รับทุเรียน)
           ประพจน์ "ถ้านายแดงซื้อทุเรียนแล้วนายแดงจะได้รับทุเรียน" ยังเป็นจริงอยู่

          จะเห็นว่ากรณีนี้นายแดงไม่ได้ซื้อทุเรียน นายแดงจึงไม่ได้รับทุเรียน
          จะเห็นว่ากรณีที่ ก เป็นจริง ข เป็นเท็จ ข้อความ ก  →  ข จะเป็นเท็จ กรณีอื่นๆ นอกจากนี้ ก  →  ข เป็นจริง

          เขียนแสดงด้วยตารางได้ดังนี้

	ก	ข	ก → ข
กรณีที่ 1	จริง	จริง	จริง
กรณีที่ 2	จริง	เท็จ	เท็จ
กรณีที่ 3	เท็จ	จริง	จริง
กรณีที่ 4	เท็จ	เท็จ	จริง

[กลับหัวข้อหลัก]

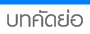
           ซึ่งเขียนแทนด้วยสัญลักษณ์  "⇔"  การเชื่อมประพจน์ ก กับ ข  ด้วย  ⇔  ซึ่งเขียนแทนด้วย ก ⇔ ข มีความหมายว่า  ก เป็นเหตุของ ข และในขณะเดียวกัน ข ก็เป็นเหตุของ ก  ด้วย ถ้าพูดตามภาษาตรรกวิทยาก็คือ ก ⇔ ข  มีความหมายเดียวกันกับ (ก → ข) ^  (ข → ก)  เช่น
            ก  แทน  สมชายไปงานเย็นนี้
            ข  แทน  สมศรีไปงานเย็นนี้

            ก ⇔ ข  แทน ถ้าสมชายไปงานเย็นนี้แล้ว (จะได้) สมศรีไปงานเย็นนี้ด้วย และถ้าสมศรีไปงานเย็นนี้แล้ว (จะได้)  สมชายไปงานเย็นนี้ด้วย
            สมมุติเหตุการณ์ว่า สุพจน์รู้จักสมชายและสมศรี และสุพจน์ได้กล่าว ประพจน์ ก ⇔ ข เราจะพิจารณาคำกล่าว ก ⇔ ข  ของสุพจน์ว่าเป็นจริงหรือเท็จได้ 4 กรณีคือ

            กรณีที่ 1   
            ก  เป็นจริง  เมื่อสมชายไปงานเย็นนี้
            ข  เป็นจริง  เมื่อสมศรีไปงานเย็นนี้
            จะได้ (ก → ข), (ข → ก) เป็นจริงทั้งคู่
            แสดงว่า (ก → ข) ^  (ข →ก) เป็นจริง ดังนั้น ก → ข เป็นจริง
            กรณีที่ 2
            ก  เป็นจริง   เมื่อสมชายไปงานเย็นนี้
            ข  เป็นเท็จ  เมื่อสมศรีไม่ไปงานเย็นนี้
             จะได้  (ก →ข) เป็นเท็จ,  (ข →ก) เป็นจริง
            แสดงว่า  (ก →ข) ^  (ข →ก)  เป็นเท็จ ดังนั้น ก ⇔ข  เป็นเท็จ
            กรณีที่ 3   
            ก  เป็นเท็จ  เมื่อสมชายไม่ไปงานเย็นนี้
            ข  เป็นจริง  เมื่อสมศรีไม่ไปงานเย็นนี้
            จะได้  (ก →ข)  เป็นจริง,  (ข →ก)  เป็นเท็จ
            แสดงว่า  (ก →ข) ^ (ข →ก) เป็นเท็จ  ดังนั้น ก ⇔ ข  เป็นเท็จ
            กรณีที่ 4   
            ก เป็นเท็จ เมื่อสมชายไม่ไปงานเย็นนี้
            ข เป็นเท็จ เมื่อสมศรีไม่ไปงานเย็นนี้
             จะได้ (ก →ข), (ก →ข) เป็นจริงทั้งคู่
            แสดงว่า (ก →ข) ^  (ข →ก) เป็นจริง ดังนั้น ก ⇔ ข เป็นจริง

            เขียนแสดงด้วยตารางได้ดังนี้

	ก	ข	ก ⇔ ข
กรณีที่ 1	จริง	จริง	จริง
กรณีที่ 2	จริง	เท็จ	เท็จ
กรณีที่ 3	เท็จ	จริง	เท็จ
กรณีที่ 4	เท็จ	เท็จ	จริง

[กลับหัวข้อหลัก]