การที่เริ่มต้นทฤษฎีว่าด้วยกราฟนี้ เกิดขึ้นในราวปี  พ.ศ. 2279  คือ เมื่อออยเลอร์ นำปัญหาการเดินข้ามสะพานในเมืองเคอนิกสเบอร์ก ประเทศปรัสเซีย อันเป็นปัญหาเก่าแก่ที่ยังไม่เคยมีใครแก้ตกมาก่อนขึ้นมาพิจารณา ปัญหาดังกล่าวเป็นปัญหาเกี่ยวกับการเดินข้ามสะพานเจ็ดสะพาน ซึ่งเชื่อมโยงระหว่างฝั่งกับเกาะ และเกาะกับเกาะปัญหามีว่าเราจะเดินจากจุดใดจุดหนึ่งข้ามสะพานต่างๆ ให้ครบทุกสะพาน โดยเดินข้ามแต่ละสะพานเพียงครั้งเดียวแล้วกลับมาถึงจุดเดิมได้หรือไม่
          ออยเลอร์แทนแผ่นดิน อันได้แก่ฝั่งแม่น้ำกับเกาะด้วยจุดสี่จุด และแทนสะพานทั้งเจ็ดด้วยเส้นเจ็ดเส้น เชื่อมโยงจุดทั้งสี่ตามที่มีสะพานเชื่อมโยงแผ่นดิน ซึ่งแทนด้วยจุดเหล่านั้น
         รูปที่ได้นี้ก็คือกราฟแสดงการเชื่อมโยงแผ่นดินส่วนต่างๆ ด้วยสะพาน คงจะไม่ผิดหากเราจะกล่าวว่ากราฟรูปนี้ เป็นกราฟรูปแรกที่ถูกนำมาใช้ในการศึกษาทฤษฎีว่าด้วยกราฟ
          ปัญหาเกี่ยวกับการเดินข้ามสะพานนั้น เมื่อแปลงมาเป็นภาษาของทฤษฎีว่าด้วยกราฟก็กลายเป็นปัญหาที่ว่า เราจะเริ่มต้นจากจุดใดจุดหนึ่ง ลากทับรอยเส้นต่างๆ ในกราฟรูปนี้ให้ครบทุกเส้น เส้นละครั้งเดียว แล้วในที่สุดลากมาบรรจบที่จุดตั้งต้นได้หรือไม่
          ออยเลอร์มิได้จำกัดการแก้ปัญหาทำนองนี้ กับกราฟรูปนี้เพียงรูปเดียว เขาพิสูจน์ทฤษฎีบทซึ่งอาจนำไปใช้กับกราฟรูปใดๆ ก็ได้ การลองแก้ปัญหาในทำนองที่กล่าวไว้ข้างต้นกับรูปกราฟคงจะช่วยให้เราเข้าในทฤษฎีบทของออยเลอร์ได้ดีขึ้น
          ในกราฟรูป ก.  ถ้าเราตั้งต้นจากจุดใดจุดหนึ่ง แล้วลากทับรอยเส้นกราฟไปในทางใดทางหนึ่งเรื่อยๆ ไป ในที่สุดเราจะกลับมาถึงจุดเดิมได้โดยลากผ่านเส้นต่างๆ ครบทุกเส้น และเส้นละครั้งเดียว สำหรับกราฟรูป ข.  นั้นเราก็อาจตั้งต้นจากจุดใดๆ ลากทับรอยเส้นต่างๆ ไปเรื่อย ให้ครบทุกเส้น เส้นละครั้งเดียว แล้วกลับมาบรรจบที่จุดเดิมได้ไม่ยากนัก แต่เราคงพบอุปสรรคในการลากทับรอยเส้นของกราฟรูป ค.
          เพื่อความสะดวกในการกล่าวข้อความในตอนต่อๆ ไป เราจะเรียกกราฟใดๆ ที่เราอาจเริ่มต้นจากจุดใดจุดหนึ่งลากทับรอยเส้นของมันไปเรื่อยๆ ให้ครบทุกเส้น เส้นละครั้งเดียว แล้วในที่สุดกลับมาบรรจบที่จุดเดิมนี้ว่า กราฟที่ลากได้ ขอให้สังเกตว่าในกราฟแต่ละรูปที่เราลากได้นั้น จำนวนเส้นที่เราลากเข้าหาจุดใดๆ ย่อมเท่ากันกับจำนวนเส้นที่เราลากออกจากจุดนั้นๆ เสมอไปแสดงว่าจำนวนของเส้นที่พบกันที่จุดใดๆ ต้องเป็นจำนวนคู่เสมอ ดังนั้นกราฟที่ลากได้แต่ละรูปจำต้องมีจำนวนของเส้นที่พบกันที่แต่ละจุดเป็นจำนวนคู่ หากกราฟใดมีจุดสักจุดหนึ่ง หรือหลายๆ จุด ซึ่งเป็นที่พบกันของเส้นต่างๆ ที่มีจำนวนเส้นเป็นเลขคี่  กราฟนั้นย่อมไม่เป็นกราฟที่ลากได้
          เนื่องจากในกราฟแสดงสะพานตามปัญหาข้างต้น จุดต่างๆ เป็นที่พบกันของเส้น 3 เส้นบ้าง 5 เส้นบ้าง กราฟนี้จึงไม่ใช่กราฟที่ลากได้  ดังนั้นคำตอบของปัญหาการเดินข้ามสะพานข้างต้นก็คือ เราจะเดินข้ามสะพานตามเงื่อนไขดังกล่าวไม่ได้
         นอกจากในการศึกษาปัญหาเกี่ยวกับการลากเส้นตามรอยเส้นกราฟดังได้กล่าวมาแล้ว จำนวนของเส้นที่พบกันที่แต่ละจุดของกราฟ ยังมีบทบาทในการศึกษาปัญหาอย่างอื่นอีกด้วย ในภาษาของทฤษฎีว่าด้วยกราฟ เราเรียกจำนวนของเส้นที่พบกันที่จุดใดๆ ของกราฟว่า ดีกรี  ของจุดนั้น เช่น แต่ละจุดในกราฟรูป ก. เป็นจุดที่มีดีกรี 2 ส่วนกราฟรูป ข. ประกอบด้วยจุดที่มีดีกรี  2  สี่จุด  กับจุดที่มีดีกรี 4 หนึ่งจุด  ดังนั้น เราอาจกล่าวข้อสรุปข้างต้นเสียใหม่ด้วยภาษาของวิชาทฤษฎีด้วยกราฟได้ว่า   ในกราฟที่ลากได้ จุดทุกจุดต้องมีดีกรีเป็นเลขคู่
          ข้อน่าคิดต่อไปก็คือ บทกลับของข้อสรุปข้างบนนี้เป็นจริงหรือไม่  คือถ้ากราฟรูปหนึ่งมีแต่จุดที่มีดีกรีเป็นเลขคู่ กราฟรูปนั้นจำต้องเป็นกราฟที่ลากได้เสมอไปหรือไม่ เราจะพบว่าบทกลับนี้ไม่จำเป็นต้องเป็นจริงเสมอไป เช่น ถ้าสะพานเชื่อมโยงเกาะกับฝั่ง ดังรูป          
          เราจะพบว่ากราฟแสดงการเชื่อมโยงแผ่นดินทั้งสี่ด้วยสะพาน เป็นกราฟซึ่งแต่ละจุดมีดีกรีที่ 2 แต่กราฟนี้มิได้เป็นรูปที่ติดต่อเป็นชิ้นเดียวกัน จึงไม่เป็นกราฟที่ลากได้  ดังนั้นคุณสมบัติอีกอย่างหนึ่ง ซึ่งกราฟที่ลากได้จะต้องมีเสมอไปก็คือ การมีลักษณะติดต่อเป็นชิ้นเดียว
          ทฤษฎีบทว่าด้วยกราฟที่ลากได้ ซึ่งออยเลอร์พิสูจน์ไว้กล่าวว่า กราฟรูปหนึ่งรูปใด จะเป็นกราฟที่ลากได้ก็ต่อเมื่อกราฟนั้นติดต่อเป็นชิ้นเดียว และจุดทุกจุดมีดีกรีคู่เท่านั้น ปัจจุบันนี้เราเรียกกราฟเช่นนี้ว่า กราฟแบบออยเลอเรียน (Eulerien)
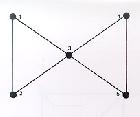
          ปัญหาเกี่ยวกับการลากทับรอยเส้นกราฟอีกประเภทหนึ่ง ซึ่งคล้ายกับปัญหาข้างต้น ปัญหาประเภทนี้มีว่า เราจะลากทับรอยเส้นกราฟไปเรื่อยๆ โดยให้ผ่านจุดต่างๆ  ของกราฟนั้นทุกจุด จุดละครั้งเดียว แล้วในที่สุดกลับมาบรรจบที่จุดเดิมได้หรือไม่  ถ้าเราลองพิจารณากราฟในรูป  ก. ข. ค. ในตัวอย่างข้างต้น เราจะพบว่ากราฟรูป ก. กับ ค. นั้นเราทำได้ ส่วนกราฟรูป  ข. นั้น เราจะลากไม่ได้ วิธีลากทับรอยกราฟ  รูป ค. ให้ผ่านทุกจุด จุดละครั้งเดียว และกลับมาถึงจุดเดิมนั้นเราอาจทำได้ตามวิธีใดวิธีหนึ่ง  ดังแสดงในรูป
          กราฟซึ่งเราสามารถลากทับรอยเส้นให้ผ่านทุกจุด จุดละครั้งเดียวและกลับมาบรรจบที่จุดเดิมได้ เราเรียกว่า กราฟแบบแฮมิลโทเนียน (Hamiltonian) ตามชื่อของเซอร์ วิลเลี่ยม โรแวน แฮมิลทัน นักคณิตศาสตร์ชาวอังกฤษ ซึ่งเป็นผู้หยิบ
ปัญหาเช่นนี้ขึ้นพิจารณา สาเหตุที่ทำให้เราลากให้ผ่านทุกจุดของกราฟ ข. จุดละครั้งเดียวไม่ได้ก็คือจุดๆ หนึ่งในกราฟรูปนี้มีคุณสมบัติพิเศษบางประการ ในรูปกราฟ ข. นี้  หากเราลบจุดหมายเลข 3 และลบทุกเส้นที่ต่อกับจุดนี้ออกเสีย เราจะได้กราฟที่เป็นสองส่วนแยกจากกัน เราเรียกจุดเช่นนี้ว่า จุดตัด จุดตัดจึงเป็นทางผ่านเพียงทางเดียว ที่เชื่อมต่อกราฟสองชิ้น ถ้าเริ่มต้นจากจากจุดใดจุดหนึ่งแล้วลากให้ผ่านทุกๆ จุด  ในกราฟเราย่อมต้องลากผ่านจุดตัดถึงสองครั้งเป็นอย่างหนึ่ง เราจึงสรุปได้ว่ากราฟที่มีจุดตัดย่อม ไม่เป็นกราฟแบบแฮมิลโทเนียน บทกลับของข้อสรุปนี้ไม่เป็นจริง กล่าวคือกราฟที่ไม่มีจุดตัดเลย แต่ไม่เป็นกราฟแบบแฮมิลโทเนียนก็มี 
          นักคณิตศาสตร์ยุคปัจจุบัน ได้พยายามค้นหาเงื่อนไขที่สะดวกต่อการใช้เป็นเกณฑ์พิจารณาว่ากราฟรูปใดรูปหนึ่งเป็นกราฟแบบแฮมิลโทเนียนหรือไม่ แต่ก็ยังไม่มีผู้ใดค้นพบเงื่อนไขที่ดีเท่าเทียมกับเงื่อนไขที่ใช้ในการพิจารณาว่า กราฟเป็นแบบออยเลอเรียนหรือไม่ เช่น มีผู้พบว่ากราฟใดๆ ที่มีสามจุดขึ้นไปและติดต่อกันเป็นชิ้นเดียว ถ้าผลรวมของดีกรีของจุด ที่ไม่ได้อยู่ติดกันแต่ละคู่ไม่น้อยกว่าจำนวนจุดทั้งหมดในกราฟนั้น กราฟนั้นย่อมเป็นแบบแฮมิลโทเนียน ส่วนที่ยังไม่ค่อยจะดีนักของทฤษฎีบทนี้ก็คือ เราไม่สามารถใช้ทฤษฎีบทนี้เพียงบทเดียว ตรวจสอบว่ากราฟเป็นแบบแฮมิลโทนเนียนหรือไม่ได้ทุกรูป เพราะกราฟแบบแฮมิลโทเนียนบางรูปที่ไม่เป็นไปตามเงื่อนไขของทฤษฎีบทนี้ก็มี เช่น รูปทางซ้ายมือ เป็นกราฟแบบแฮมิลโทเนียน ซึ่งจุดคู่ที่ห่างกันมีดีกรีรวมกันได้น้อยกว่าจำนวนของจุดในรูป