|
Advertisement
Advertisement
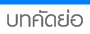
ฟังก์ชันของ exponential เป็นฟังก์ชันที่ใช้ได้ง่าย และยังเป็นธรรมชาติที่สามารถวิเคราะห์ได้ง่าย เพราะสามารถทำการ derivatives และ integrates ได้ง่าย
ฟังก์ชันอัตราการเจริญเติบโตหรือการเปลี่ยนแปลงแบบเอ็กซ์โพเนนเชียลที่น่าสนใจ คือ
|
เมื่อ
|
x ( t )
|
คือ ค่าผลลัพธ์ที่เวลา t
|
|
|
|
A
|
คือ ค่าสูงสุด หรือค่า x เมื่อ t = o
|
|
|
e
|
คือ ฐานของลอการิทมิกธรรมชาติ = 2.71828
|
|
|
T
|
คือ ค่าคงตัวของเวลา
|
|
|
t
|
มีหน่วยเป็นวินาที
|
|
|
|
|
|
|
|
|
เมื่อทำให้สเกลสูงสุดเป็น 1 ได้กราฟ
|
และค่า T นี้ เรียกว่า ค่าคงตัวเวลา
ซึ่งถ้า t = T จะได้ค่า e-1 หรือ 1/2.718 ซึ่งมีค่าเท่ากับ 0.368
นั่นคือ เมื่อเวลาค่า T จะลดลงเหลือ 0.368 ของค่าสูงสุด
และถ้า t = 2T, 3T, 4T ...... ก็จะมีค่าเป็น
e-2, e-3 , e-4,.........ซึ่งจะมีค่าเป็น 0.135, 0.0498, 0.0183 ตามลำดับ
หากนำกราฟผลักกลับเป็น
|
x ( t ) = 1 - e-t/T
ผลลัพธ์ที่ได้จะเป็นดังกราฟ
|
|
|
|
ที่มา: รศ. ยืน ภู่วรวรรณ, สำนักบริการคอมพิวเตอร์ มหาวิทยาลัยเกษตรศาสตร์
|
Advertisement
|
เปิดอ่าน 5,426 ครั้ง |
เปิดอ่าน 115,439 ครั้ง |
เปิดอ่าน 12,202 ครั้ง |
เปิดอ่าน 29,761 ครั้ง |
เปิดอ่าน 27,926 ครั้ง |
เปิดอ่าน 32,616 ครั้ง |
เปิดอ่าน 77,437 ครั้ง |
เปิดอ่าน 15,035 ครั้ง |
เปิดอ่าน 42,281 ครั้ง |
เปิดอ่าน 27,618 ครั้ง |
เปิดอ่าน 28,826 ครั้ง |
เปิดอ่าน 48,831 ครั้ง |
เปิดอ่าน 67,087 ครั้ง |
เปิดอ่าน 5,102 ครั้ง |
เปิดอ่าน 15,921 ครั้ง | |
|
เปิดอ่าน 8,250 ☕ คลิกอ่านเลย |
เปิดอ่าน 43,266 ☕ คลิกอ่านเลย | 
เปิดอ่าน 41,743 ☕ คลิกอ่านเลย | 
เปิดอ่าน 21,227 ☕ คลิกอ่านเลย | 
เปิดอ่าน 19,117 ☕ คลิกอ่านเลย | 
เปิดอ่าน 28,826 ☕ คลิกอ่านเลย | 
เปิดอ่าน 24,306 ☕ คลิกอ่านเลย |
|
≡ เรื่องน่าอ่าน/สาระน่ารู้ ≡ 
เปิดอ่าน 14,093 ครั้ง | 
เปิดอ่าน 18,526 ครั้ง | 
เปิดอ่าน 10,800 ครั้ง | 
เปิดอ่าน 10,502 ครั้ง | 
เปิดอ่าน 9,173 ครั้ง |
|
|
ค้นหาทุกอย่างในเว็บครูบ้านนอก :
TAGS ที่เกี่ยวข้อง >> 
