นักคณิตศาสตร์ของโลกที่น่าสนใจ!!! "วงรอบของสุริยุปราคาจะเกิดทุก 18 ปี 10 วัน 8 ชั่วโมง

นักคณิตศาสตร์ของโลกที่น่าสนใจ!!!
สาระ :	ทักษะกระบวนการทางคณิตศาสตร์
กลุ่มสาระฯ :	คณิตศาสตร์
ข้อมูลระดับ :	ประถมศึกษา

เธลิส
กรีกโปราณอาจมีนิยามที่แตกต่างจากประเทศกรีกในปัจจุบันอาณาของชนชาติโบราณเปลี่ยนแปลงอยู่ตลอดเวลา ตามอารยธรรม กรีกโบราณจึงครอบคลุมไปถึงตรุกีทางใต้ไปจนถึงอิตาลี

จากความเป็นจริงในปัจจุบันพบว่า การเกิดสุริยุปราคาจะไม่เป็นรายคาบ แต่จะขึ้นกับตำแหน่งของโลก การคำนวณสุริยุปราคาจึงต้องกระทำโดยอาศัยคณิตศาสตร์ที่ซับซ้อนขึ้น และยังไม่มีใครพบหลักฐานที่เด่นชัดว่าชาวบาบิโลเนียน ทำนายการเกิดสุริยปราคาด้วยหลักฐานและทฤษฎีอะไร ซึ่งก็อาจเป็นได้ว่า ชาวบาลิโลเนียนมีการคำนวณบนพื้นฐานของวิทยาการที่เป็นไปได้ เกี่ยวกับพื้นผิวโลก

เธลีสเป็นนักปริชญาชาวกรีก เป็นนักวิทยาศาตร์ และคณิตศาสตร์ที่มีชื่อเสียง เธลิส เป็นชาวเมืองไมล์ตุส(Miletus) ซึ่งทางตะวันตกเฉียงใต้ของตรุกี เธลีสใช้ชีวิตอยู๋ในช่วงเวลาประมาณ 600 ปี ก่อนคริตศตวรรศอย่างไรก็ดีผลงานของเธลิสที่เป็นข้อเขียนไม่หลงเหลือเป็นหลักฐานเลย แต่จากหลักฐานที่กล่าวอ้างถึงเธลิสโดยนักคณิตศาสตร์ผู้อื่นพบว่า เธลีสได้เขียนตำราเกี่ยวกับการหาทิศและการเดินเรือ การกล่าวอ้างถึงเอลิสที่นำสนใจเรื่องหนึ่งคือ เธลิสได้ทำนายการเกิดสุริยปราคาได้ถูกต้องในปี 585 BC แต่เขาอ้างถึงของรอบเวลาที่เกิดสุริยปราคาซึ่งจะเกิดขึ้นในประมาณ 19 ปี แต่ก็เป็นการยากเพราะสุริยปราคาจะเกิดเป็นช่วงพื้นที่หนึ่ง การทำนายสุริยปราคาจึงอาศัยประสบการณ์การคาดเดาที่อยู่บนพื้นฐานของความรู้ เชื่อกันว่าเธลิสใช้ข้อมูลที่มีมาจากชาวบาบิโลเนียน ที่กล่าวว่าวงรอบของสุริยุปราคาจะเกิดทุก 18 ปี 10 วัน 8 ชั่วโมง

หลังจากเกิดสุริยปราคาในวันที่ 28 พฤษภาคม 585 BC ฮีโรโคกุสได้เขียนข้อความบันทึกไว้ว่า   "อยู่ ๆ กลางวันก็พลอยเป็นกลางคืนไปในทันที เหตุการณ์ครั้งนี้ได้รับการทำนายบอกไว้ก่อนโดย เธลีส ซึ่งเป็นชาวไมล์ตุส"   การเกิดสุริยปราคาครั้งนี้สร้างความประหลาดใจ และความตื่นเต้นอย่างยิ่ง

 

จนกระทั่งปัจจุบันก็ย้งไม่หลักฐานใดที่จะบอกได้ว่าเธลีสใช้ทฤษฎีหรือคำนวณได้อย่างไร นักคณิตศาสตร์ในภายหลังเลื่อว่า การที่เธลีสทำนายได้ถูกต้องเพราะ เธลีสเป็นผู้สังเกตุและศึกษาทางเปลี่ยนเปลี่ยนของท้องฟ้ามีการจดบันทึกการเปลี่ยนแปลง และดูการเคลื่อนไหวของดวงดาวบนท้องฟ้า จะทำให้ทราบการเคลื่อนที่ในตำแหน่งต่าง ๆ

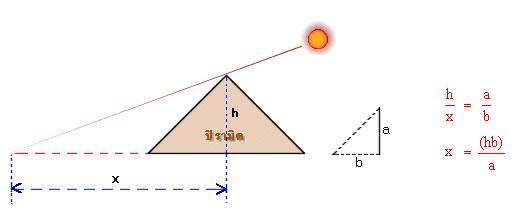
เธลิสได้มีโอกาสดินทางไปประอิยิปต์ ขณะนั้นศิลปวิทยาการที่อียิปต์รุ่งเรือง โดยเฉพราะคณิตศาสตร์ในสาขาวิชาเรขาคณิต เธลีสได้เสอนวิฮีการคำนวณความสูงของปิรามิดที่อียิปต์ โดยการวัดระยะทางของเงาที่เกิดขึ้นที่ฐานของปิรามิด กับเงาของหลักที่รู้ความสูงแน่นอนวิชาการของเธลีสคือการใช้ รูปสามเหลียมคล้าย การที่เธลีสได้มีโอกาสเดินทางไปอียิปต์ ทำให้เธลิสนำเอาวิชาการทางด้านคณิตศาสตร์มายังกรีก และมีลูกศิษย์ พลาโต (Plato) ได้เขียนถึงเธลีสในผลงานของเขาว่า เธลีสได้แสดงออกถึงความเป็นครูและได้นำวิทยาการมาถ่ายทอด ความคิดของเธลีสเน้นในเชิงปฏิบัติ

สิ่งที่เป็นผลงานและเป้ฯที่กล่าวอ้างถึงเธลีส คือ ทฤษฎีบทเกี่ยวกับเรขาคณิต   5  ทฤษฎี  คือ
วงกลมใด ๆ ถูกแบ่งออกเป็นสองส่วนเท่า ๆ กันโดยเส้นผ่านศูนย์กลาง
มุมที่ฐานของสามเหลี่ยมหน้าจั่วมีค่าเท่ากัน
เส้นตรงสองเส้นตัดกัน มุมตรงข้ามที่เกิดขึ้นย่อมเท่ากัน
สามเหลี่ยมสองรูป ถ้ามีมุมเท่ากันสองมุม และด้านเท่ากันหนึ่งด้าน สามเหลี่ยมทั้งสองคล้ายกัน
มุมภายในครึ่งวงกลมเป็นมุมฉาก 
 
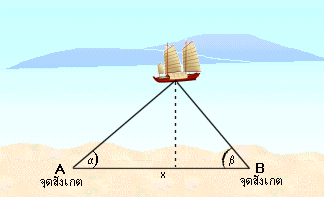
จากทฤษฎีทางเรขาคณิตในเรื่องด้านและมุม เธลิสเสนอวิธีการ วัดระยะทางเรื่องที่อยู่ในทะเลว่าห่างจากฝั่งเท่าไร โดยมีผู้สังเกตวัดระยะอยู่บนฝั่ง
เธลิสได้เสนอความเชื่อของตนเองอย่างหนึ่งว่า "ทุกสิ่งทุกอย่างคือน้ำ"  ซึ่งเป็นจุดเริ่มต้นของความคิดและค้นหาคำตอบในเรื่องวิทยาศาสตร์ โดยมีสมมุติฐานที่ต้องการพิสูจน์   เธลิสเชื่อว่า โลกลอยอยู่บนน้ำ และทุกสิ่งทุกอย่างมาจากน้ำ เขาเชื่อว่าโลกแบบเหมือนจานที่ลอยอยู่บนพื้นมหาสมุทรที่ไม่มีขอบเขตกำจัดเธลีสอธิบายการเกิดแผ่นดินไหว เหมือนจานที่ลอยอยู่บนน้ำและกระเพื่อมตามแรงน้ำ จากปริชญาของเธลิสพอสรุปได้เป็น
1.มีวัตถุสิ่งของได้มากมาย
2.มีเพียงชนิดเดียวคือ น้ำ
3.คำว่ายูนิเวอร์ส (Universe) ไม่สามารถที่อธิบายได้ในเทอมของชิ้นส่วนที่ไม่ต่อเนือง แต่อยู่ในเทอมของของที่เชื่อมโยงถึงกันที่เรียกว่า Space อย่างไรก็ตามความคิดของเธลิสในส่วนข้อ 2 และ3 ได้รับการโต้แย้งอย่างมากในเวลาต่อมาในเรื่องความถูกต้องของหลักปรัชญา และทฤษฎี


พีธากอรัส
พีธากอรัสเป็นนักคณิตศาสตร์ที่มีชื่อเสียงมาก จากหลักฐานทางประวัติศาสตร์เชื่อว่า พีธากอรัสมีอายุอยู่ในราว 582 - 500 ก่อนคริสตกาล พีธากอรัสเป็นชาวกรีก เป็นนักปรัชญา และผู้นำศาสนา พีธากอรัสมีผลงานที่สำคัญคือ เป็นนักคิด เป็นนักดาราศาสตร์ นักดนตรี และนักคณิตศาสตร์ แรกเริ่มในชีวิตเยาว์วัยอยู่ในประเทศกรีก ต่อมาได้ย้ายถิ่นพำนักไปตอนใต้ของอิตาลี ที่เมืองโครตัน (Croton) ศึกษาเล่าเรียนทางปรัชญาและศาสนาที่นั่น พีธากอรัสมีผู้ติดตามและสาวกเป็นจำนวนมาก ซึ่งเรียกว่า Pythagorean การทำงานของพีธากอรัสและสาวกจึงทำงานร่วมกัน